GNSS-Inertial State Initialization Using Inter-Epoch Baseline Residuals

Samuel Cerezo1, Javier Civera1
1Universidad de Zaragoza
Submitted to RA-L, 2025
Paper arXiv Code

Abstract

This paper proposes a novel GNSS-inertial initialization strategy that delays the use of global GNSS measurements until sufficient information is available to accurately estimate the transformation between the GNSS and inertial frames. Instead, the method initially relies on GNSS relative distance residuals. To determine the optimal moment for switching to global measurements, we introduce a criterion based on the evolution of the Hessian matrix singular values. Experiments on the EuRoC and GVINS datasets show that our approach consistently outperforms the naive strategy of using global GNSS data from the start, yielding more accurate and robust initializations.

Illustration of our GNSS-IMU initialization approach. a) Global residuals remain inactive while the system lacks informative measurements. b) At time $k^*$, the GNSS-inertial measurements provide sufficient information to meet our criterion, enabling the inclusion of global constraints for accurate alignment.

Formulation

Our goal is estimating the state $\mathbf{x}$ of a sensing platform equipped with GNSS and inertial sensors. The state consists of the device's rotation, position, linear velocity, IMU gyroscope bias, and gravity direction at different time steps. We define the general state $\mathbf{x}$ as \begin{equation} \mathbf{x} = \left[\mathbf{x}_1^\top,\mathbf{x}_2^\top, \cdots, \mathbf{x}_k^\top, \cdots ,\mathbf{x}_N^\top, {\mathbf{b}^g}^\top, {\hat{\mathbf{g}}}^\top\right]^\top~, \end{equation} where \begin{equation} \mathbf{x}_k = \left[\mathbf{R}_k^\top, {\mathbf{p}}_k^\top,{\boldsymbol{\omega}}_k^\top,{\mathbf{v}}_k^\top\right]^\top~, \end{equation}

We formulate a nonlinear optimization problem over the state variables $\mathbf{x}$, incorporating constraints from inertial preintegration and GNSS measurements. The objective is to find the optimal estimate $\hat{\mathbf{x}}$ that minimizes a joint cost function $J(\mathbf{x})$: \begin{equation} \label{eq:optimizacion_problem} \hat{\mathbf{x}} = min_{\mathbf{x}} J(\mathbf{x}) \end{equation}

This cost function aggregates several residual terms, each encoding information from a different sensor modality or physical constraint. More details about this formulation are included in the article.

Observability Analysis

To analyze the system’s observability, we construct the observability matrix $\mathcal{O}$ by stacking the Jacobians of all residuals in the cost function with respect to the state vector, as follows \begin{align} \mathcal{O} = \begin{bmatrix} \frac{\partial \mathbf{r}_{\Delta \mathbf{R}}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\Delta \mathbf{v}}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\Delta \mathbf{p}}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\text{d}}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\text{p}_i}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\text{p}_j}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\omega}}{\partial \mathbf{x}}^\top, \frac{\partial \mathbf{r}_{\mathbf{g}}}{\partial \mathbf{x}}^\top \end{bmatrix}^\top \end{align}

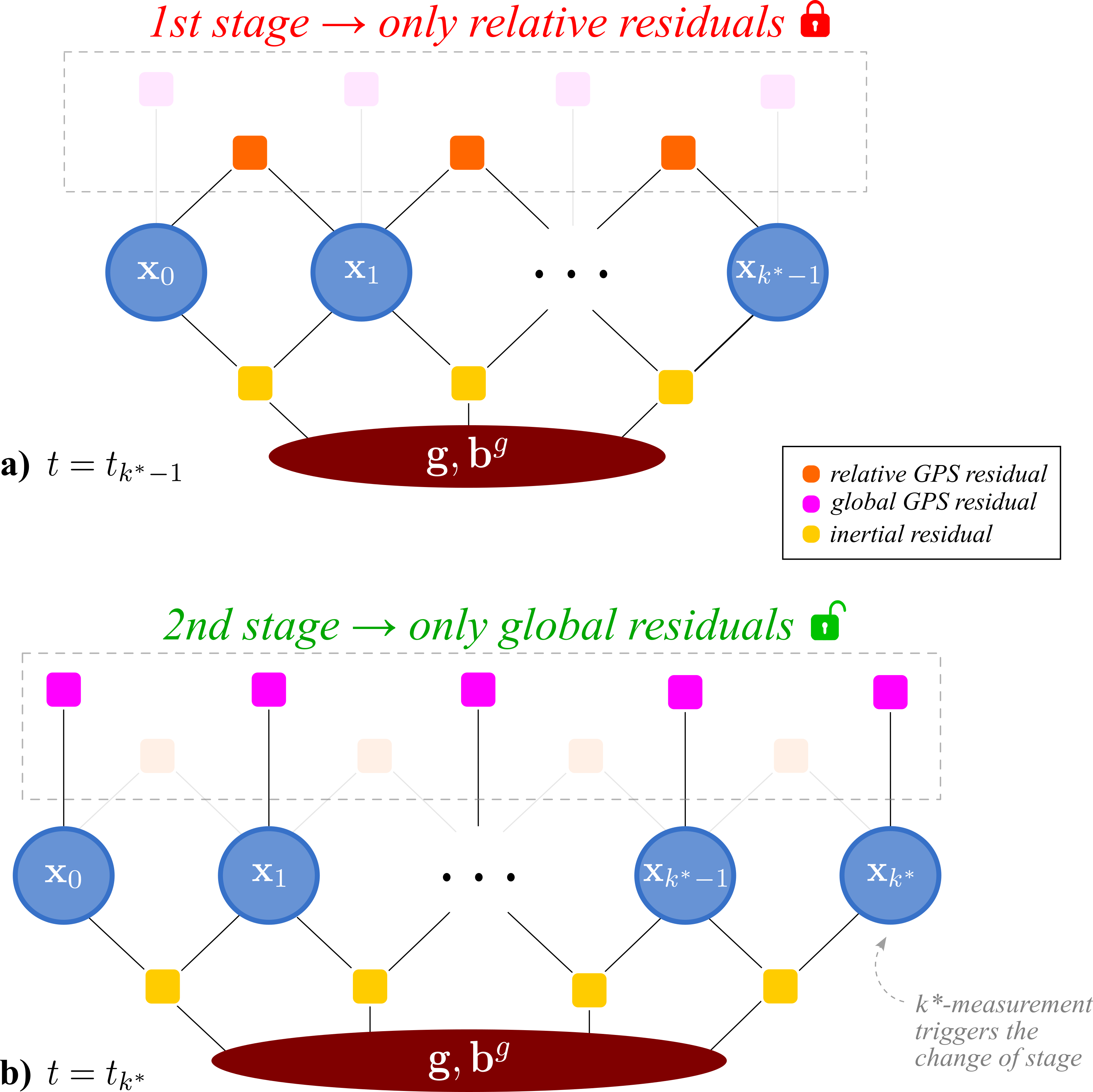
The explicit structure of the observability matrix \( \mathcal{O} \), derived from the defined residuals, reveals a maximum symbolic rank of 23 due to linear dependencies among GPS constraints. To handle this underconstrained initialization, we fix the initial pose (position, velocity, and orientation), reducing the number of estimated variables to 14. In this setup, \( \mathcal{O} \) achieves a numerical rank of 11, with remaining ambiguities linked to the second pose, gyroscope bias, and gravity direction. Rather than relying on external priors, our method exploits the coupling between IMU preintegration and GNSS data, progressively enhancing observability as the trajectory evolves. 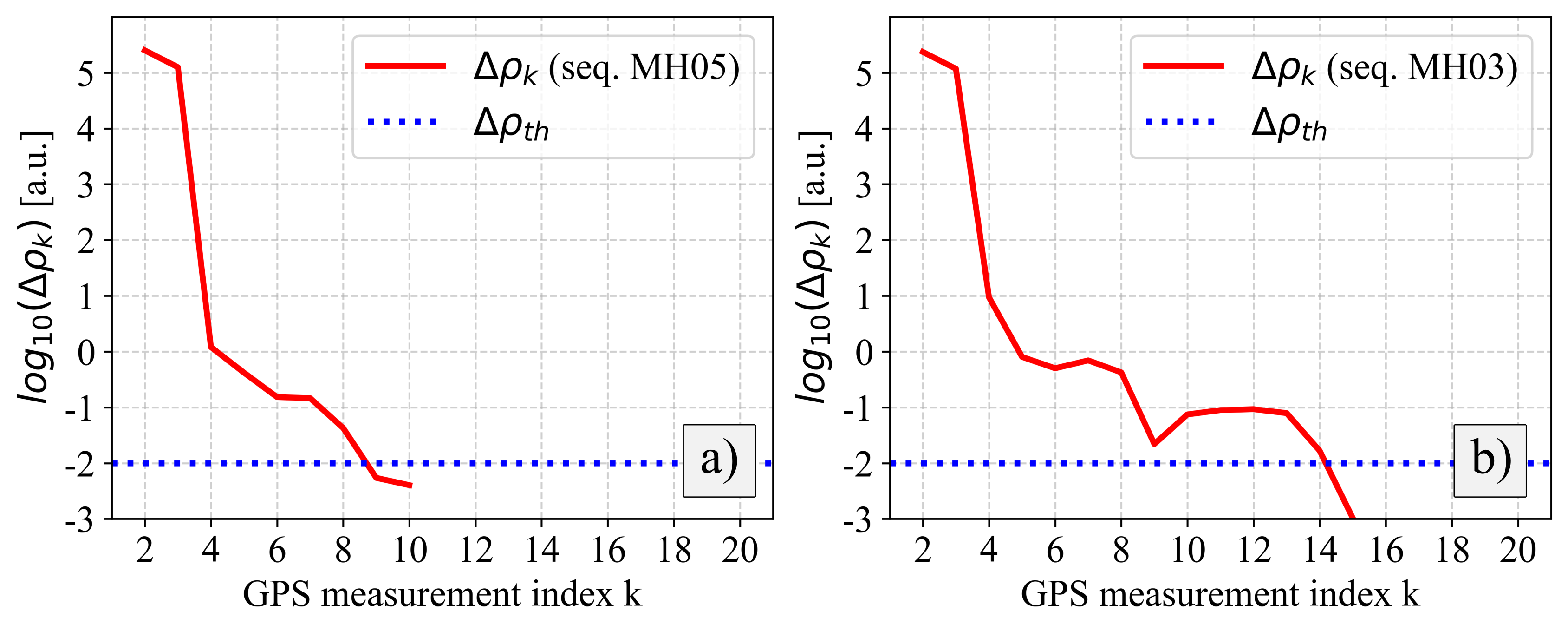To ensure robustness, we delay the activation of global GPS terms until sufficient motion renders the system observable, thereby avoiding early noise sensitivity.

Triggering criterion

To determine the triggering time index \( k^* \), we analyze the observability of the extrinsic transformation \( \mathbf{T}_{W}^{B} \) by inspecting the singular values of an approximate Hessian matrix constructed from GNSS-only residuals. These include one relative and two absolute position terms. The Hessian is built by linearizing the residuals with respect to the six parameters of \( \mathbf{T}_{W}^{B} \), and its conditioning is evaluated via singular value decomposition. We define the singular value ratio \( \rho_k = \sigma_{\max} / \sigma_{\min} \) and track its relative variation: \[ \Delta \rho_k = \left| \frac{\rho_k - \rho_{k-1}}{\rho_{k-1}} \right|. \] A low and stable \( \Delta \rho_k \) indicates that the system has become sufficiently observable. We therefore activate global GPS constraints and begin estimating \( \mathbf{T}_{W}^{B} \) only when \( \Delta \rho_k < \Delta \rho_{\mathrm{th}} \), with \( k^* \) denoting the triggering index. This strategy provides a principled, data-driven criterion to safely incorporate global information while avoiding premature sensitivity to noise. The Figure below shows the evolution of the relative change $\Delta \rho_k$ for two EuRoC sequences. When the curve drops below the observability threshold $\Delta \rho_{\mathrm{th}} = 10^{-2}$, the system is considered sufficiently constrained to support the inclusion of global position residuals in the estimation.

Example of our activation criterion for two EuRoc sequences. a) On the MH05 sequence, the criterion results in $k^*=9$ GPS measurements; b) on the MH03 sequence, it suggests $k^*=15$ GPS measurements. The dashed blue line represents the observability threshold $ \Delta \rho_{{th}}$.

BibTeX


    @article{cerezo2025gnss,
      title={GNSS-inertial state initialization by distance residuals},
      author={Cerezo, Samuel and Civera, Javier},
      journal={arXiv preprint arXiv:2506.11534},
      year={2025}
    }