Abstract
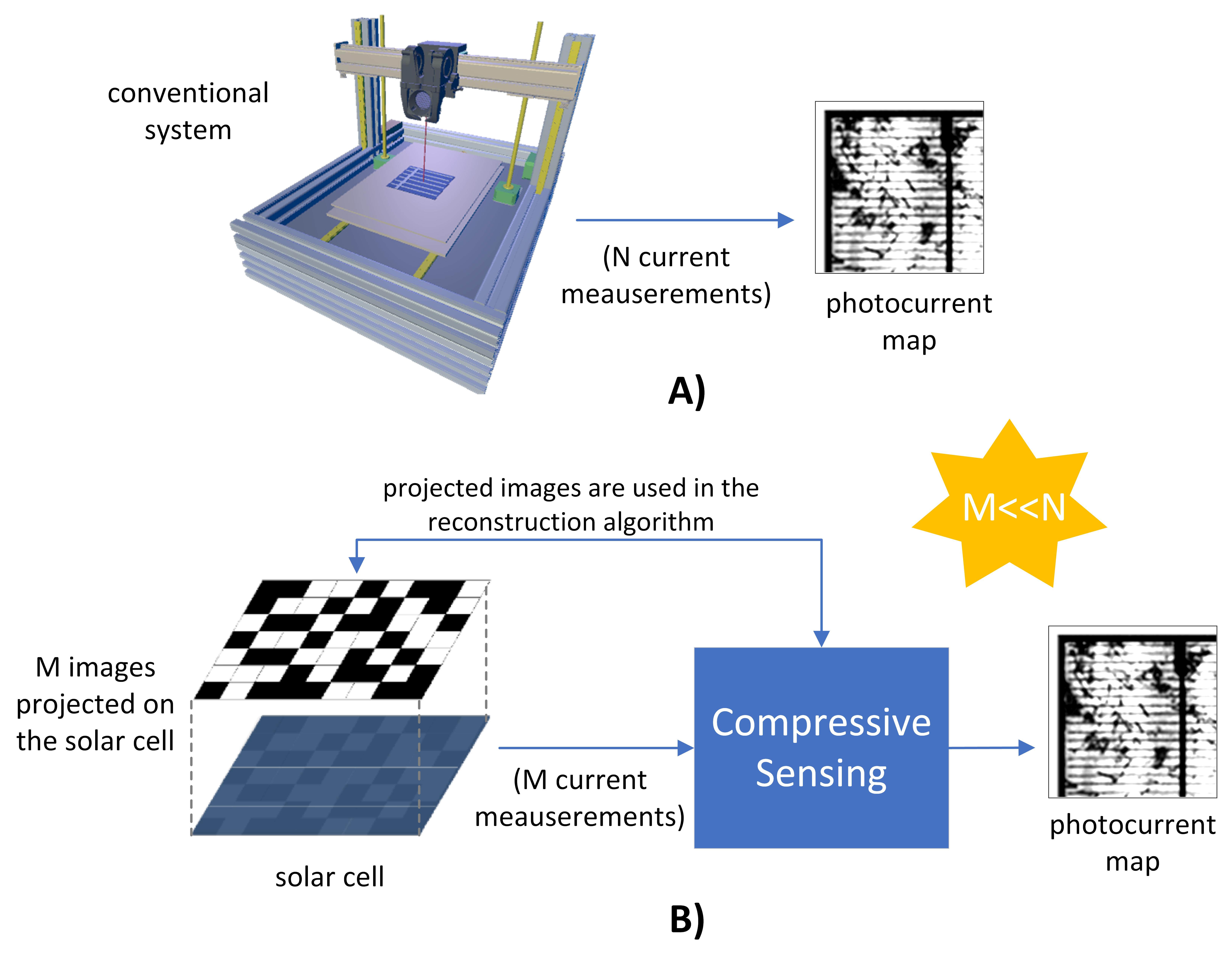
Photocurrent mapping (PM) is a non-destructive characterization method of solar cells and panels. It is used in the industry for quality control in the production of photovoltaic devices, in scientific laboratories to characterize new materials, and in photovoltaic facilities to find module failures. The PM consists of applying a laser light beam perpendicularly on a photovoltaic device, scanning the surface point by point, and measuring the induced current as a function of the position of the beam (Figure A). These systems require a high degree of mechanical stability, which leads to an increase in the characterization times when the area is large. In recent years, it has been made progress in the use of compressive sensing algorithms applied in PM tests (Figure B) in order to reduce moving parts and the measuring times. In this work we apply the compressive sensing technique to obtain a photocurrent map of Si photovoltaic devices. Results are compared with the ones obtained by the conventional technique.
Formulation
The current map for a photovoltaic device with a standard $N$point test area corresponds to a vector $x$ represented in a given basis $\Psi$: \begin{equation} x=\sum_{i=1}^N \psi_i s_i = \Psi s \end{equation}The signal $x$ is called K-sparse in $\Psi$ basis if only $K$ components of the vector $s$ are non-zero and the others, i.e. $N-K$ components, are zero. If one could know in advance in which base the signal to be measured is sparse, it would be sufficient to measure the $K \ll N$ values corresponding to the coefficients of the signal in that base, i.e. it would be sufficient to make $K$ measurements. We denote $y_j$ ($j=1,\dots,M$) as each of the measurements of the signal $x$. Each measurement will be a linear combination of the values of $x$, so it can be thought of as an inner product between $x$ and a vector $\phi_j$ ($j=1,\dots,M$). Rearranging the vectors $\phi_j$ in the rows $\phi_j^T$ forms a matrix $\Phi \in \mathbb{R}^{M\mathrm{x}N}$ called measurement matrix. Substituting, we obtain: \begin{equation} y=\Phi x = \Phi\Psi s=\Theta s \end{equation} The matrix $\Theta \in \mathbb{R}^{M\mathrm{x}N}$ must satisfy two conditions: the principle of restricted isometry and the incoherence property. The direct construction of the matrix $\Phi$ such that $\Theta=\Phi\Psi $ fulfills both conditions is very difficult to achieve, however both can be achieved with high probability by means of a random $\Phi$ matrix of Bernouli type.
Once $\Phi$ has been defined and the $M$ measurements have been made, the algorithm should be able to obtain the values of the vector $s$ by solving the inverse problem $y = \Theta s$. This is an ill-conditioned problem, i.e., there are many and significantly different solutions, so the algorithm is asked to impose some constraint on $s$. Two alternatives are examined next: minimizing the $l_1$ norm and minimizing the Total Variation (TV). After the minimization process, the map corresponding to the photovoltaic device $x$ is obtained by $x = \Psi s$.
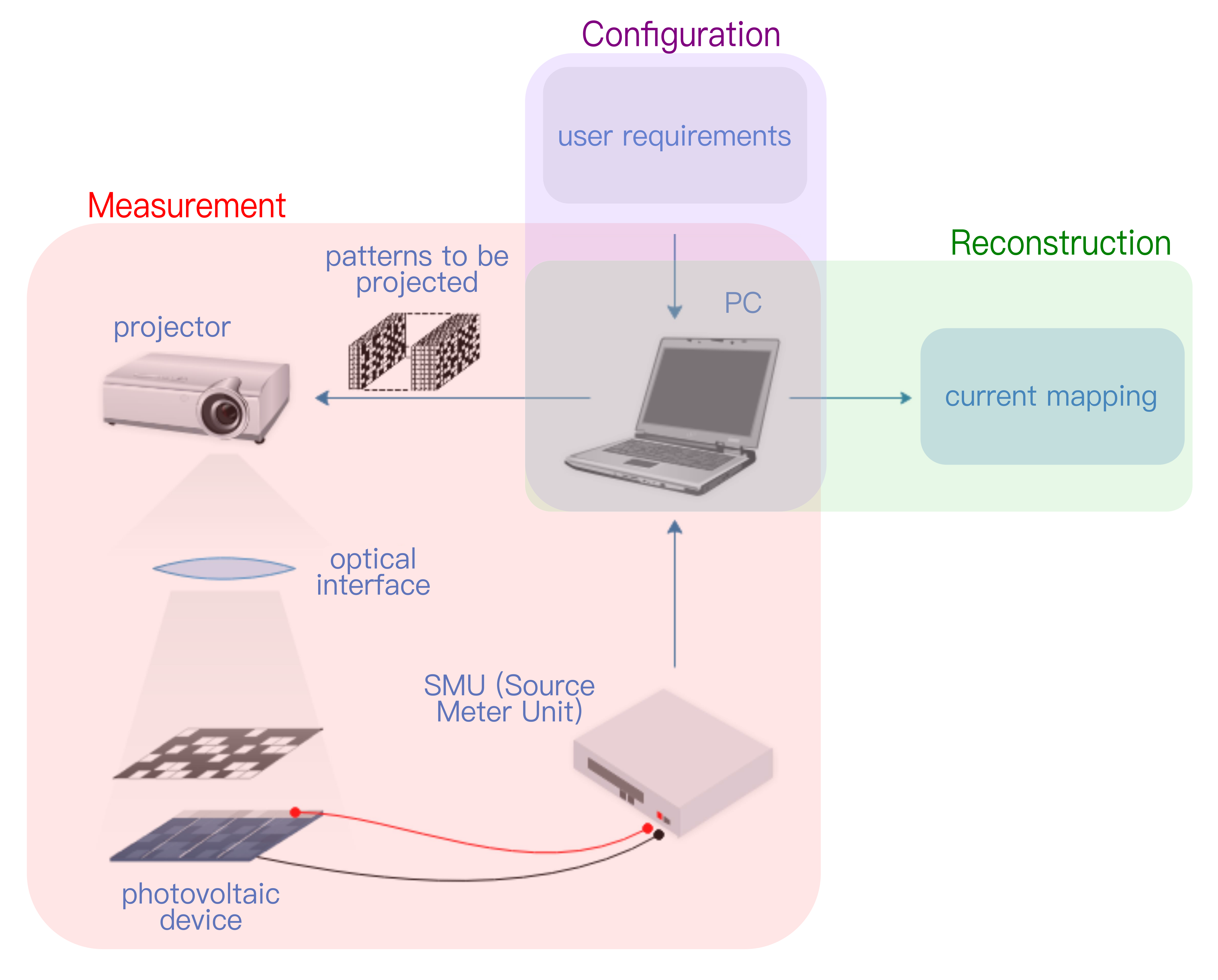
The scheme of experimental set-up is shown in the next figure, where the three stages are displayed in different colors.
The user starts a measurement using the graphical interface stored in the computer (PC). The projector is used for imaging the patterns on the cell. A lens is used to modify the size of projected patterns. Finally, the current values are obtained by a SMU (Source Meter Unit) Keithley 2400 and stored in the PC. After this process, an optimization algorithm returns the photocurrent map throw a minimization function.
a) Measurement processThe measurement process consist of obtaining $M$ measurements of a signal $x$, which in this case represents the photocurrent map of the cell. Each measurement is obtained by performing the product between the signal $x$ and a matrix $\phi_j$ ($j=1,\dots,M$). Each one of these $M$ matrices has 64 rows by 64 columns and is randomly generated with values 1 and 0. In turn, this matrix is equivalent to an image called \emph{pattern} that consists of small squares called \emph{pixels}. A black pixel corresponds to the value 0, and similarly a white pixel corresponds to 1. The randomly generated pattern is projected onto the solar cell.
Next figure shows the measurement process represented in mathematical form, in order to visualize the relationship between the measurement process and the mathematical problem to be solved. In this figure the process is carried out as an example taking $M=4$ measurements by means of four 3x3 patterns. In the following section the results are shown in real samples using 64x64 patterns.
The purple square represents the actual PM of cell $x$ which is rearranged as a column vector. The projected patterns, or equivalently the $\phi_j$ matrices, are rearranged as rows to form the measurement matrix $\Phi$. By projecting the $M$ patterns onto the cell and acquiring the $M$ photocurrent values, what is being done mathematically is a multiplication between the measurement matrix $\Phi$ and the actual PM of the cell $x$, to obtain the measurement vector $y$. Therefore, the aforementioned inverse problem $\Phi x=y$ is expressed. The latter is solved in the reconstruction process, to find the photocurrent map of the cell.
b) Reconstruction processThe mathematics involved in compressive sensing ensures that a good representation of the photocurrent map $x$ is achieved, without knowing in advance the basis on which this representation is sparse. As we saw, the inverse problem $\Phi x = y$ is reformulated as $\Phi x= \Phi \Psi s = \Theta s = y $. This new matrix $\Theta$ results from the multiplication between $\Phi$ and $\Psi$, therefore it still fulfills the necessary conditions for the compressive sensing process. Now, it remains to know which is the proper basis $\Psi$ where the PM representation is sparse.
Result on a Si-solar cell Next figure A shows a real photo of the solar cell with a 3 $mm^2$ rectangular defect placed on the surface, in order to observe if the CS system is able to detect it. The PM obtained by the CS system is shown in B. For this measurement, 64x64 pixel patterns are projected, so that each pixel has an area of 310x310 $\mu m^2$. The reconstruction of the PM is performed by minimizing the Total Variation (TV) and using the DCT as the mathematical basis. For this reconstruction, 50% of the patterns were used. This value is determined as follows: \begin{equation} percentage [\%] = \frac{M}{N}*100%. \end{equation}- $M$ is the number of patterns projected during the measurement process.
- $N$ is the number of pixels each pattern has. For example, a 64x64 pattern has $N$ = 64*64 = 4096 pixels.
BibTeX
@INPROCEEDINGS{cerezo-compressive,
author={Cerezo, Samuel and Córdoba, Matías Andrés and Quintián, Fernando Pérez},
booktitle={2023 Argentine Conference on Electronics (CAE)},
title={Compressive Sensing Mapping System for Spatial Characterization of Photovoltaic Devices},
year={2023},
volume={},
number={},
pages={1-6},
}