A Closed-Form Solution to Full Visual–Inertial State Initialization

Abstract

We present a closed-form initialization method that estimates the complete visual–inertial state —including velocity, gravity, and IMU biases—without iterative optimization. Our formulation leverages small-rotation and constant-velocity approximations to make the problem analytically tractable while preserving the key coupling between motion and inertial measurements. Experiments on the EuRoC dataset demonstrate that this approach achieves accuracy comparable to optimization-based baselines while being several orders of magnitude faster.

Method

Rotation and Gyroscope Bias

The method begins by estimating the gyroscope bias analytically under a commutative rotation model. Assuming small inter-frame rotations, Rodrigues’ formula allows linearization of IMU preintegration:

\( R_{ij} \approx \prod_{k=i}^{j-1} \mathrm{Exp}((\tilde{\omega}_k - \mathbf{b}_g)\Delta t) \)

This leads to a direct closed-form expression:

\( \mathbf{b}_g \approx -\frac{1}{L\Delta t}\mathrm{Log}\!\left[\!\!\left(\!\!\prod_{k=i}^{j-1}\mathrm{Exp}(\tilde{\omega}_k\Delta t)\!\!\right)^\top R_{ij}\!\!\right] \)

We further derive two constant-velocity models, with and without preintegration, enabling robust bias recovery even with noisy or short IMU segments.

Closed-Form Initialization

Once the gyroscope bias is known, the remaining states (velocity, gravity, accelerometer bias) are estimated from linear constraints derived from IMU–camera relations. The stacked system can be written as:

\( \Xi \mathbf{x} = \mathbf{s} \)

where \(\Xi\) encodes integrated inertial terms and feature observations, and \(\mathbf{x}\) includes gravity, velocity, and accelerometer bias. The least-squares solution is obtained by SVD, monitoring rank changes to verify observability.

Observability-Driven Trigger

Initialization is activated once sufficient motion renders the system observable. A two-stage strategy combines a parallax threshold to detect translational excitation and a Hessian-based test monitoring the stability of singular values:

\( \Delta\rho_j = \left|\frac{\rho_j - \rho_{j-1}}{\rho_{j-1}}\right|, \quad \text{activate if } \Delta\rho_j < \Delta\rho_{\mathrm{th}} \)

Experiments

The proposed method is evaluated on the EuRoC MAV dataset, which provides synchronized stereo and IMU data. We compare the closed-form estimator against optimization-based methods across 11 sequences, analyzing accuracy, robustness, and runtime.

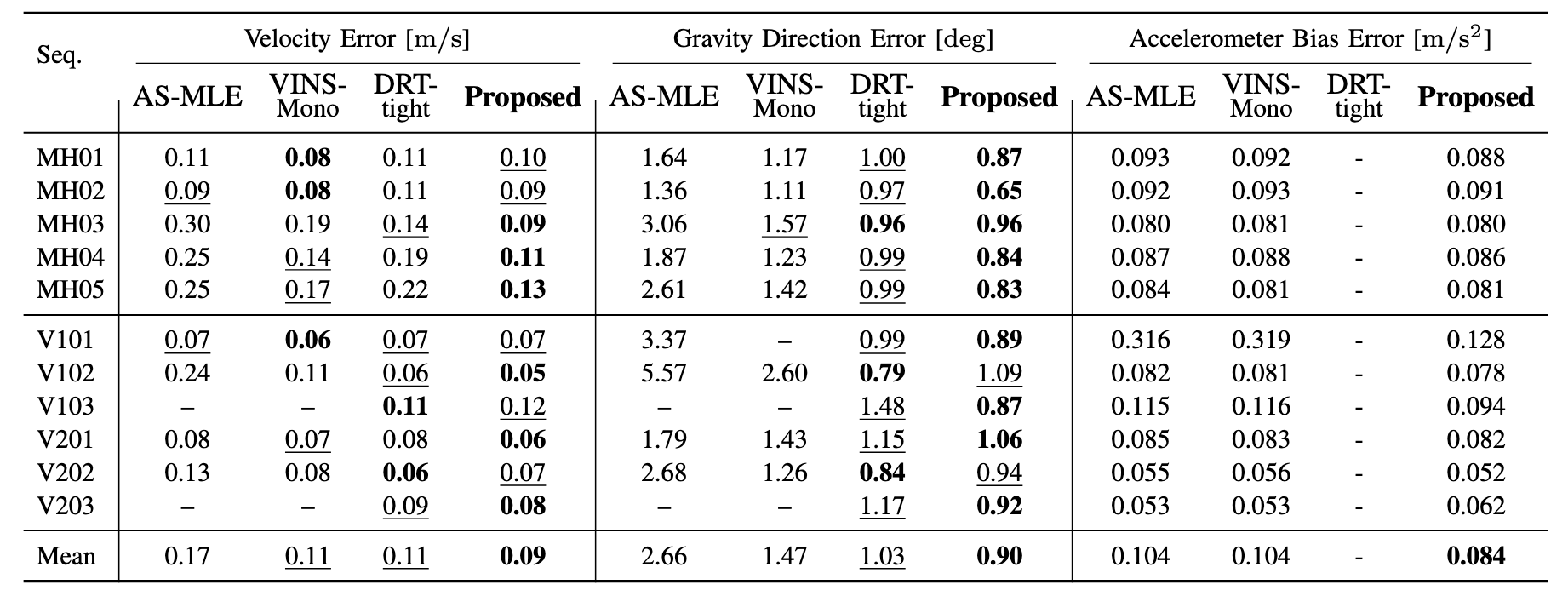
Across EuRoC, the closed-form initialization achieves the lowest average velocity error (0.09 m/s), gravity-direction error (0.9 deg), and accelerometer-bias error (0.084 m/s²). Runtime analysis confirms improvements of over two orders of magnitude compared with nonlinear baselines.

Average runtime per module compared with state-of-the-art methods.

Conclusion

We proposed the first fully analytical initialization that recovers the complete visual–inertial state without nonlinear solvers. Leveraging small-rotation and constant-velocity assumptions enables a tractable yet accurate solution that drastically reduces computation time. Our method provides a robust, lightweight initialization suitable for real-time VI-SLAM systems and resource-constrained platforms.

BibTeX


@article{2026VIinit,
  title={A Closed-Form Solution to Full Visual--Inertial State Initialization},
  author={Cerezo Samuel, Seong Hun Lee and Civera Javier},
  journal={},
  year={2026}
}

A Closed-Form Solution to Full Visual-Inertial State Initialization